Implementation of Routh's stability analysis using C++
This program can be helpful in finding whether a control system (e.g, used in Cars, Robots, etc.,) is stable or not using Routh's stability criterion. Here C++ programming language is used.
This program can be used in control systems applications. The Control system is a vast area. In airplanes, automobiles, and submarines, they play a major role. The stability in a control system is essential in driving these systems. It is used to predict Longevity, good performance, and ability to reach the steady-state. This program can be used to find out the stability of a small or subpart or a whole system. First, we need to understand how the analysis is done. To find the stability of the system using Routh's criterion we need the characteristic equation of the system.
The programming is done using c++ language in the visual studio environment. Initially, we need to get the characteristic equation of the control system which is nth order continuous system. i.e for a car as shown below. Every control system has a characteristic equation.
![]()
where n=7 and the Routh's array for the characteristic equation is

Here the coefficients an,an-1 up to an-5 are seen in the first two rows of the Routh array. The b1,b2,b3,c1,c2,c3 up to mn-1 elements are found using the following formulas.

In the program, at first, the coefficients of the characteristic equation are inputted and stored in the array. As shown below, the first row elements of the Routh array are stored in a[]and the second-row elements in b[] respectively. To ease the calculation two variable names a[],b[] are used for the first two rows in the program.
cout << "Enter the coefficient of the characteristic equation upto degree 7\n"; /*input the coefficient values*/
for (n = 0; n < 8; n++)
{
cin >> w[n];
}
for (n = 0; n < r; n++) /*for loop for storing first row elements*/
{
a[n] = w[i - (2 * n)];
}
for (n = 0; n < u; n++) /*for loop for storing second row elements*/
{
b[n] = w[i - 1 - (2 * n)];
}
By using this Routh array, three conditions are checked. They are stable, Marginally stable, and unstable. The element of the third,fourth and fifth rows c[],d[],e[], are calculated using the above prescribed formula. In the program, the for loop is used for that. After finding the elements we go for analysis.
1) If anyone element of the first column of the Routh array is zero, then the system is marginally stable. To make it nonzero, the derivative of the previous row is used. The coefficients of the calculated derivative are added into the same row for further calculation as shown in the script.
for (n = 0; n < 3; n++) /*for loop for third row elements calculation*/
{
if (b[n] != 0)
{
c[n] = ((b[0] * a[n + 1]) - (a[0] * b[n + 1])) / b[0];
}
if (c[0] == 0) /*if the elements of the thrid row is zero,calculate it using derivative of previous row*/
{
i=highest degree entered;
for (n = 0; n < 3; n++)
{
i--; c[n] = i * b[n]; i--;
}}}
The shown method of code is used for the calculation of each elements from b1,b2,b3,c1,c2,c3 up to mn-1 in the program.
2) When any one of the elements in the first column of the Routh array is negative, then the system is unstable.
3) If all the elements in the first column are positive and nonzero then it is said to be stable.
The limitations in using the Routh array are that it can be used only for linear time-invariant systems. i.e, the output of the system doesn't depend on time. e.g, seismic sensors, Speech processing, etc. It is valid only if the characteristic equation is algebraic. If any one of the coefficients of the characteristic equation is complex or contains a power of 'e', this criterion cannot be applied.
The test run is shown below,
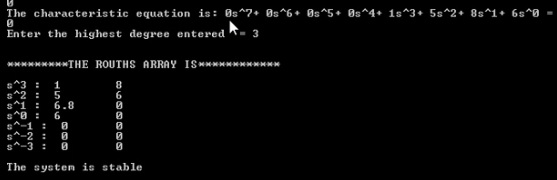
Submitted by Mohamed Adila.A (Adila)
Download packets of source code on Coders Packet
Comments