Kruskal's Algorithm for Minimum Spanning Tree in C++
A packet in C++ which helps finding minimum spanning tree. It is subset of connected edge-weighted graph that connects all vertices together without cycles and minimum total edge weight
The packet helps in finding a minimum spanning tree out of an input graph. A graph may contain cycles and loops in it but a tree never contains a cycle in it. The tree formed consists of all the vertices mentioned in the graph but it's not the same case with edges given in the graph. The packet can be used to find out the minimum path connecting all the points having the least cost of all possible paths in the graph.
The packet uses the standard library in C++, bits/stdc++.h. Kruskal's Algorithm is a greedy approach that finds a connection between all the points which is of the least total weight. The algorithm subsequently selects the next minimum edge in the graph and checks whether using it will create a loop in the tree or not if it does not then the edge is selected.
The packet has three functions:
1. Function Sorter. It is used to sort the edge sequences in increasing order of their weights. It is custom sorting function.
2. Function get_parent. When an edge is selected, one of the points is made the parent of another point of the edge. The function helps to prevent the creation of a cycle in the tree. If an edge is selected with both the points having the same parent the corresponding edge is not selected.
3. Function get_MST. It is the parent function that uses the get_parent function in its definition. Selects one edge at a time uses get_parent function on each edge and decides whether to add it to the Minimum Spanning Tree.
The packet asks for 3 types of inputs.
1. Number of vertices in the graph
2. Number of edges in the graph
3. List of edges of the form {G1, G2, X}, where G1, G2 are two vertices having an edge between them of weight 'X'.
The packet outputs the list of edges and corresponding edge weights which will be included to form an MST.
Sample Input / Ouput
Sample Graph
-1613977024-331.jpg)
Inputs on the basis of above graph
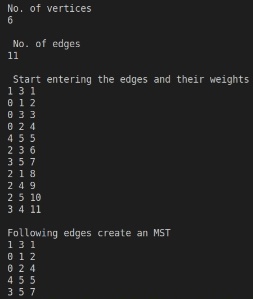
The resultant tree structure without any loops with least cost
-1613977964-331.jpg)
Submitted by Dhruv Prakash Raipure (DhruvRaipure)
Download packets of source code on Coders Packet
Comments