Travelling Salesman Problem using AI Genetic Algorithm in C++
An AI based Genetic Algorithm implementation in C++ to find the solution of the travelling salesman problem optimally.
Travelling Salesman Problem is an important real-life problem. In this, we have to find out the best route to be taken by a salesman, so that he can travel to all the destinations by the shortest possible distance (or cost). This finds a real-life application in delivery systems like that in Amazon, Flipkart, Zomato and Swiggy for example and also can be used in car-pooling applications such as Uber to find the shortest route.
The original algorithm used to find the best solution is very time-consuming. If we implement it, then the program may even take days or weeks to find the best possible answer to our problem. So, by using Artificial Intelligence, we can improve the speed of the program such that a program that would have taken days or weeks normally can be solved within a few minutes using the special technique of Genetic Algorithms. Although this does not guarantee the best solution, it always gives a solution which is very close to the best solution, but the speed efficiency is really great, so this is used as a substitute to the original algorithm to achieve faster performance.
For this program, we are given an input distance map which represents the cost of travelling from one city to the other.
Currently I have set the following as the input distance map. We can easily modify the code to let the user input the distance map, by taking input as we do in a matrix.
vector distance_map = {
{INF, 10, 3, 2, 5, 6, 7, 2, 5, 4},
{20, INF, 3, 5, 10, 2, 8, 1, 15, 6},
{10, 5, INF, 7, 8, 3, 11, 12, 3, 2},
{3, 4, 5, INF, 6, 4, 10, 6, 1, 8},
{1, 2, 3, 4, INF, 5, 10, 20, 11, 2},
{8, 5, 3, 10, 2, INF, 6, 9, 20, 1},
{3, 8, 5, 2, 20, 21, INF, 3, 5, 6},
{5, 2, 1, 25, 15, 10, 6, INF, 8, 1},
{10, 11, 6, 8, 3, 4, 2, 15, INF, 1},
{5, 10, 6, 4, 15, 1, 3, 5, 2, INF}
};
NOTE: INF represents a very large number. It means if we go to that position, it cannot lead to optimal path.
The program outputs multiple routes which can lead to the shortest possible total distance. This repeats for some number of generations, (here I have chosen 4).
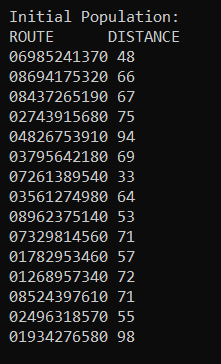
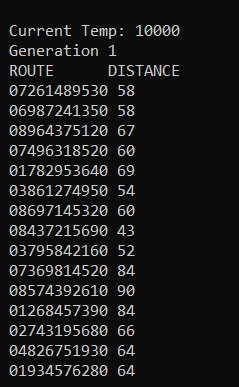
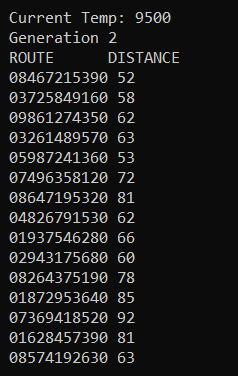
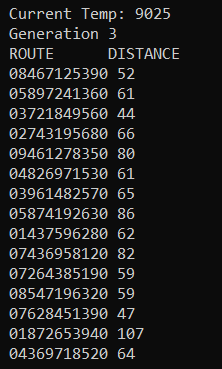
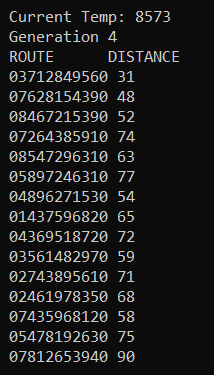
After this, the program ends. We see that the smallest possible distance is 31 for the route 0->3->7->1->2->8->4->9->5->6->0.
Thus, we got the required route such that the distance is minimal and that too in a few seconds.
Submitted by Gaurav Sawant (GauravSawant)
Download packets of source code on Coders Packet
Comments