Understanding and Implementing AdaBoost Algorithm in Python

By ABISHEK KRISHNAPRASAD

AdaBoost algorithm intuition and implementation in Python on Iris dataset for multi-class classification

Ensemble methods refer to a group of models working in unity to solve a common problem. Rather than depending on a single model for the best solution, ensemble learning utilizes the advantages of several different methods to countervail the other models’ individual weaknesses. This results in a better predictive performance than could not be obtained from any of the constituent learning algorithms alone, this can be understood by a weak algorithm creating weak classifiers, which then can be combined and what we may get is a stronger classifier.

AdaBoost, which abbreviates for ‘Adaptive Boosting’, is a machine learning meta-algorithm (a way of combining other algorithms) which can be used in conjunction with many other types of learning algorithms to improve performance, it was initially used to increase the efficiency of binary classifiers.

The Algorithm:

Let’s assume we have a sample/dataset and have them divided into the training set, test set and some classifiers, these classifiers are trained on overlapping subsets of the training set and not as in cross validation sets, The AdaBoost assigns a weight that determines the probability for which a particular observation is likely to appear in the training set. Hence, the weights assigned are straight forward and those with higher probabilities are assigned higher weights, this leads to assigning higher weights to misclassified data, since they represent a larger part of the classifiers with the objective that the following classifiers will be most likely trained better on the data.

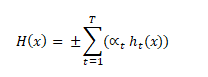
The above is the equation for a binary classifier, it encompasses the weighted sum of the outputs ht of the weak classifier T, equal to the output of the weights of the classifier t, αt

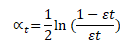
Here, εt is the error term of the classifier t, let’s visualize a graph corresponding to the relation between the alpha value and the error,

#import the necessary libraries
import numpy as np
import matplotlib.pyplot as plt

error = np.arange(0,1,0.01)
alpha_t = 1/2*np.log((1-error)/error) #equation for alpha t

plt.plot(error, alpha_t)
plt.title('Visualizing Alpha')
plt.xlabel('Error')
plt.ylabel('Alpha')

Visual Summary:

• The classifier weight grows exponentially as the error approaches 0. Better classifiers are given exponentially more weight.
• The classifier weight is zero if the error rate is 0.5. A classifier with 50% accuracy is no better than random guessing, so we ignore it.
• The classifier weight grows exponentially negative as the error approaches 1. We give a negative weight to classifiers with worse than 50% accuracy.

Weights:

The weights for the first classifiers are equally initialized and normalized over the size of the dataset(1/n) and from the second classifier, the following formula is used to recursively compute the weights,

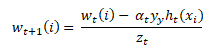
The variable wt is a vector of weights, with one weight for each training example in the training set. ‘i’ is the training example number, this equation updates the ith training example in our dataset, here, wt is represented as a distribution. This just means that each weight w(i) represents the probability that training example i will also be a part of the training set.

To make it a distribution, all of these probabilities should add up to 1. To ensure this, we normalize the weights by dividing each of them by the sum of all the weights, zt. So, for example, if all of the calculated weights added up to 10, then we would divide each of the weights by 10, so that they sum up to 1 instead.

This vector is updated for each new weak classifier that’s trained. wt refers to the weight vector used when training classifier ‘t’, this equation needs to be evaluated for each of the training samples ‘i’ (xi, yi). Each weight from the previous training round is going to be scaled up or down by this exponential term.

Interpretation:

• If yt*ht(xi) is positive and α>0, then it is a strong classifier and hence the weight assigned is small.
• If yt*ht(xi) is positive and α<0, then it is a weak classifier and hence the weight assigned is large.
• If yt*ht(xi) is negative and α>0, then it is a strong classifier and hence the weight assigned is small.
• If yt*ht(xi) is negative and α<0, then it is a strong classifier and hence the weight assigned is small.

Python Implementation:

The Dataset:

The Dataset used here is a well-known inbuilt dataset available in the sci-kit library, known as the Iris dataset, that is most commonly used for multi-class classification, it has three classes and 50 samples per class.

Implementing AdaBoost:

The necessary modules from sci-kit library is imported and a classifier is used, I've used Random Forest Classifier (a collection of decision trees, which is a part of ensemble learning algorithms), but the default classifier used in AdaBoost is a decision tree classifier.

from sklearn import datasets #for iris dataset
from sklearn.ensemble import AdaBoostClassifier

dataset = datasets.load_iris()
X = dataset.data
y = dataset.target

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

from sklearn.ensemble import RandomForestClassifier #default classifier is decision ree
random_forest = RandomForestClassifier(n_estimators = 10, criterion = 'entropy', random_state = 0)
adaboost =AdaBoostClassifier(n_estimators=50, base_estimator=random_forest,learning_rate=1)

classifier = adaboost.fit(X_train, y_train)
y_pred = classifier.predict(X_test)

from sklearn import metrics
print('Final Accuracy:',metrics.accuracy_score(y_test, y_pred))

Conclusion:

From the predictions, we witness an accuracy of 93% thanks to our AdaBoost algorithm, we can further tune the parameters and try with a range of other classifiers such as Naive Bayes or Support Vector Machines to get even better results, Hope you found the implementation helpful and gained an intuitive understanding of the Adaptive Boosting Algorithm and it's efficacy on improving the performance of classifiers.